Пиляк К. Ю., студентка физико-инженерного факультета 3 курса 2 группы
Уравнение Лапласа можно решать аналитически, либо с помощью различных методов численного решения. Одним из эффективных итерационных методов является метод SOR (successive over relaxation). Однако, при достаточно большом количестве узлов, его программная реализация с использованием вложенных циклов демонстрирует серьезное падение производительности.
Одним из способов ускорения расчетов для «больших» задач является использование возможностей системы MATLAB по работе с матрицами. Чтобы избежать обращения к соседним элементам матрицы решений можно использовать циклические сдвиги матрицы (функция circshift). Тогда необходимость во вложенных циклах пропадает.
Проведем сравнительный расчет одной и той же задачи по численному решению уравнения Лапласа методом SOR в MATLAB.
Первая реализация алгоритма использует стандартный подход с перебором узлов вычислительной сетки во вложенных циклах.
tic;
n=130;
h=1/(n-1);
x = 0:h:n;
v = zeros(n + 2, n + 2);
omega = 1;
colormap(hsv(256));
for i = 2:n+1
v(2,i)=45*x(i-1)*(1-x(i-1));
end;
for k=1:1000
for i=3:n+1
for j=3:n+1
v(i,j)=v(i,j)+omega/4*(v(i+1,j)+v(i-1,j)+v(i,j-1)+v(i,j+1)-
4*v(i,j));
end
end
end;
surf(v(2:n+1,2:n+1));
toc;
При количестве узлов n = 100 алгоритм выполняется на стандартном компьютере приблизительно 3,5 с.
Вторая реализация алгоритма использует возможности функции circshift.
tic;
n=130;
h=1/(n-1);
x = 0:h:n;
v = zeros(n + 2, n + 2);
omega = 1;
colormap(hsv(256));
for i = 2:n+1
v(2,i)=45*x(i-1)*(1-x(i-1));
end;
for i=0:1000
R = omega / 4 * (circshift(v,1) + circshift(v,-1) + circshift(v,[0,1]) +
circshift(v,[0,-1]) — 4 * v);
v(3:n,3:n)=v(3:n,3:n) + R(3:n,3:n);
end;
surf(v(2:n+1,2:n+1));
toc;
При количестве точек n = 100 второй алгоритм выполняется на стандартном компьютере приблизительно 0,58 с.
На следующем рисунке изображена производительность двух реализаций метода SOR для различного количества узлов.
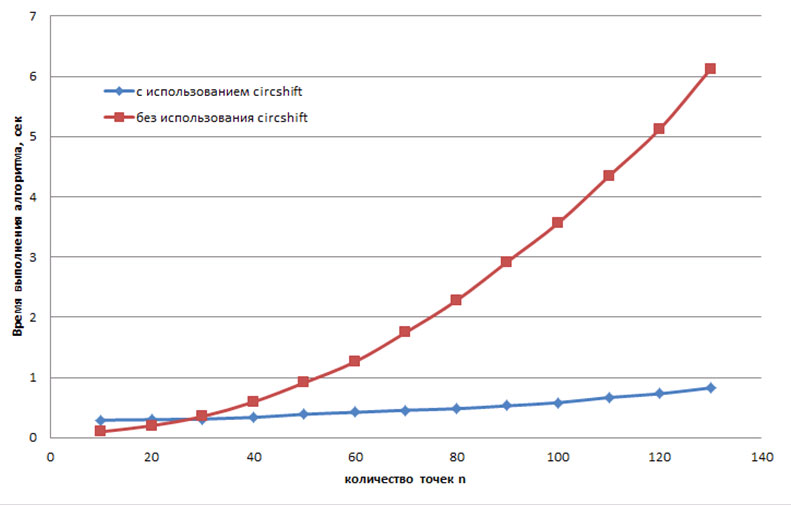
При малых n реализация алгоритма без circshift эффективнее, чем реализация с использованием circshift. Однако при n > 30 использование circshift дает лучшие результаты.
Таким образом, использование особенностей Matlab может значительно улучшить эффективность численных алгоритмов.
