Вопросы к экзамену

Дорогие женщины! Мужчины кафедры поздравляют вас с 8 марта!

Вопросы к экзамену по дисциплине «Алгоритмы вычислительной геометрии» для студентов 2 курса физико-математического факультета специальности «Прикладная математика».

Кафедра Информатики и МПИ провела 20.11.15 семинар «Облачные технологии в образовании».  Интерес к дискуссии проявили специалисты из Мозыря и Калинкович.

Авторы: Гриневич В.С., Пейсахович О.И., Василенко Д.В.

Уравнение Пуассона – дифференциальное уравнение в частных производных. С его помощью можно описать некоторые физические процессы и явления, такие как стационарное поле температуры и электростатическое поле.
Перед нами стояла задача исследования потенциала электростатического поля. Весь процесс можно описать уравнением Пуассона, которое было решено в математическом пакете MATLAB прямым методом и методом верхней релаксации. В нашей работе прямой метод обозначен Matrix, а метод верхней релаксации обозначен как Relax

Matrix
При решении явным методом:
• просчитали матрицу с граничными условиямиv(1,i)=45*x*(1-x);
• учли все условия для расположения неизвестных значений узлов сетки;
• записали матрицу с коэффициентами для расчетов;
• нашли решение и изобразили в 3D формате.

tic;
n=120;
h=1/(n-1);
v=zeros(n,n);
k=n-2;
t=k*k;
y=zeros(t,1);
fori=1:n
x=(i-1)*h;
v(1,i)=45*x*(1-x);
end;
q=1;

for i=1:n
for j=1:n
if v(i,j)~=0
y(q,1)=v(i,j);
q=q+1;
end
end
end

z=zeros(t,t);
for i=1:t
for j=i+1:t
if mod(i,k) == 0
z(i,j)=0;
z(j,i)=0;
else
z(i,j)=-1;
z(j,i)=-1;
end

if (j-i+1)==k+1;
z(i,j)=-1;
z(j,i)=-1;
end;

if (((j-i+1)>2) & ((j-i+1)<k+1)) & ((j-i+1)~=k+1) z(i,j)=0; z(j,i)=0; end; if j-i>k
z(i,j)=0;
z(j,i)=0;
end;

end;
z(i,i)=4;
end;

w=inv(z)*y;
r=reshape(w,k,k);
colormap(hsv(256));
surf(r), view(-126,32);
toc;

Relax
Поскольку на практике обычно встречаются «большие» задачи, то встаёт необходимость быстро находить решение, хоть даже придётся поплатиться точностью вычислений. Быстроту вычислений могу обеспечить итерационные методы, например метод верхней релаксации.
Ниже приведён пример решения уравнения Пуассона методом верхней релаксации, реализованный в MATLAB. Здесь в переменной n задаётся размерность сетки, в переменной niter задаётся количество итераций, влияющих на точность вычислений. В строке u(1,i)=45*x*(1-x) задаются начальные условия, а результат вычислений находится в переменной u. В коде программы также реализован подсчёт затраченного на вычисления времени.

tic;
n=300;
niter=1000;
h=1/(n-1);
w=1;
u=zeros([n,n]);
for i=2:n-1
x=(i-1)*h;
u(1,i)=45*x*(1-x);
end
g=zeros([n,n]);
colormap(hsv(256));
for k=0:niter
for i=2:n-1
for j=2:n-1
u(i,j)=u(i,j)+w/4*(u(i+1,j)+u(i-1,j)+u(i,j-1)+u(i,j+1)-4*u(i,j)-h*h*g(i,j));
end
end
end
surf(u);
toc;

Время, для вычисления каждого из методов, выводилось на экран, при помощи функций tic toc. Среднее для каждого значения заносилось в Excel, и строился график функций.

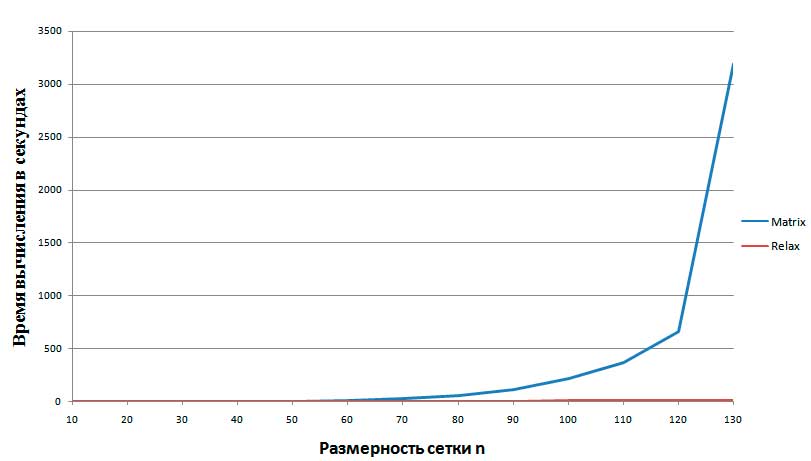
Рисунок 1: Сравнение времени вычисления явного и неявного методов.

На рисунке 1 заметно, что оба метода, в пределах размерности сетки n до шестидесяти, работают почти с одинаковой скоростью, однако с последующим ростом количества точек, метод Matrix значительно отстаёт по времени от методом Relax.
Из графика, построенного в Excel, видно, что время вычисления решения методом верхней релаксации, с большим числом разбиения сетки (n = 130), в 640 раз меньше времени вычисления прямым методом.
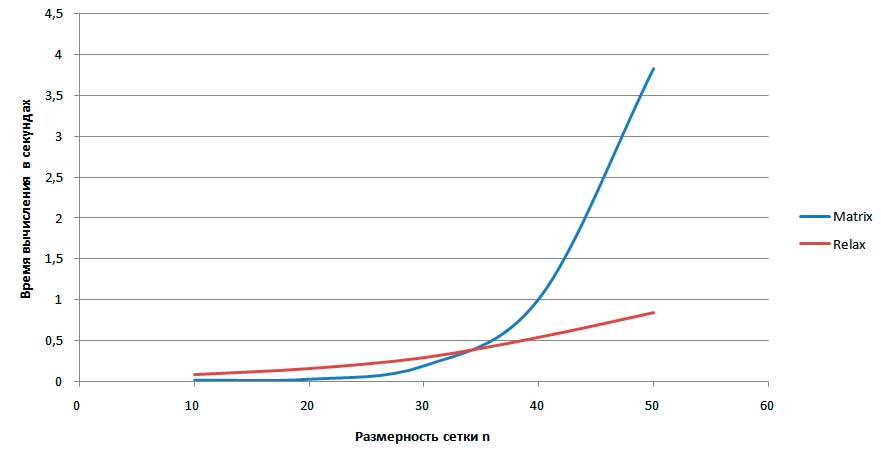
Однако для n=35 метод Matrix считает быстрее Relax, что видно на рисунке 2.

Рисунок 2: Сравнение времени вычисления явного и неявного методов при малых значениях n.

Посмотреть динамику решения можно на приведенном видео.

Таким образом, в работе проведено решение уравнения Пуассона двумя различными методами Matrix и Relax, выполнено сравнение времени вычисления каждым методом. Показано, что в случае, когда количество точек в расчетной матрице превышает величину n=35 намного выгоднее использование метода верхней релаксации.